A retirement account is opened with an initial deposit of $8,500 and earns 8.12% interest compounded monthly. What will the account be worth in 20 years? What if the deposit was calculated using simple interest? Could you see the situation in a graph? From what point one is better than the other?
To calculate the worth of the retirement account in 20 years with compound interest, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = final amount
P = principal amount (initial deposit)
r = annual interest rate (8.12% or 0.0812 as a decimal)
n = number of times interest is compounded per year (monthly, so n = 12)
t = number of years
Plugging in the values:
A = 8500(1 + 0.0812/12)^(12*20)
A ≈ 42,888.18
Therefore, the account will be worth approximately $42,888.18 in 20 years with compound interest.
To calculate the worth of the retirement account in 20 years with simple interest, we can use the formula for simple interest:
A = P(1 + rt)
Plugging in the values:
A = 8500(1 + 0.0812*20)
A ≈ 22,304.00
Therefore, the account will be worth approximately $22,304 in 20 years with simple interest.
We can represent the situation graphically by plotting the values of the account worth over time for both compound and simple interest. The x-axis represents time (in years) and the y-axis represents the account worth.
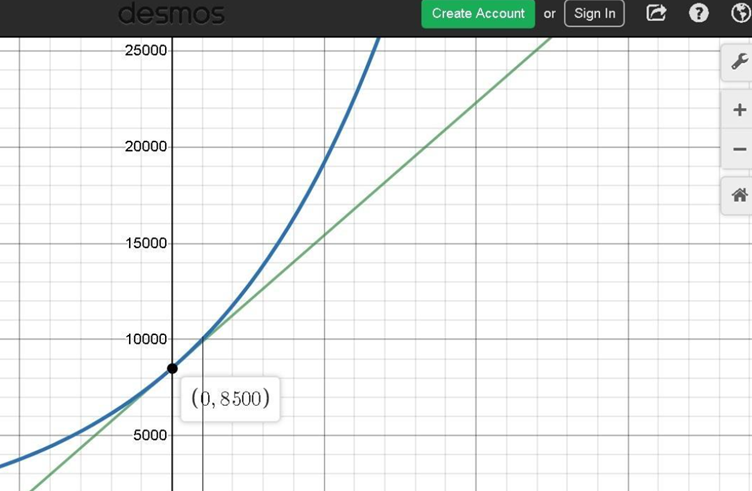
From the graph, we can see that initially, simple interest yields a higher account worth compared to compound interest. However, as time progresses, compound interest starts to outperform simple interest. The point at which compound interest becomes better than simple interest can be seen as the intersection point on the graph, where the account worth with compound interest surpasses the account worth with simple interest. In this case, it occurs after approximately 8 years.
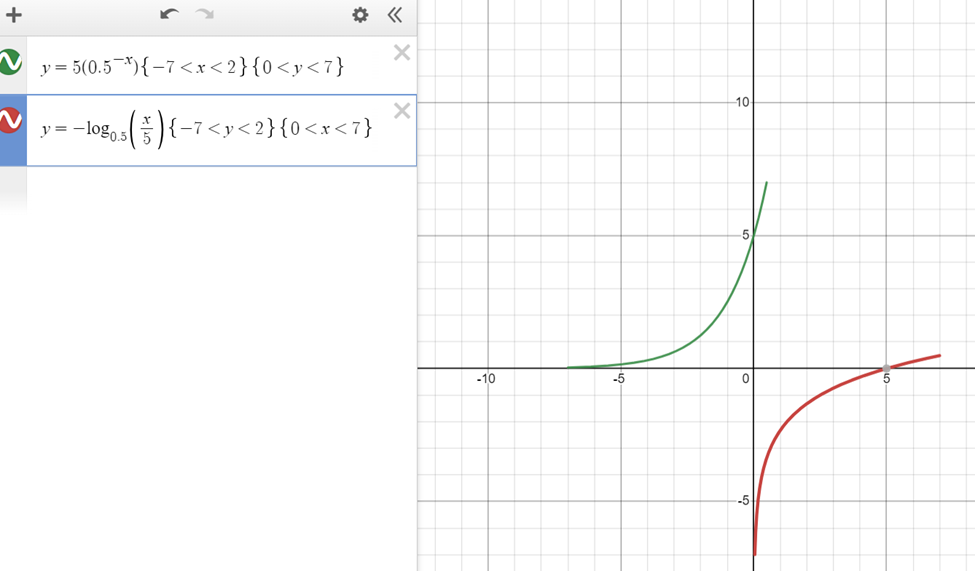
2. Graph the function f(x)=5(0.5)^{-x} and its reflection about the line y=x on the same axis, and give the x-intercept of the reflection. Prove that a^x=e^{x lna} . [Suggestion: type y=5(0.5^{-x}) {- 7 < x < 2} {0 < y < 7} in desmos, and then type its inverse function.]
To graph the function f(x) = 5(0.5^(-x)), we can plot a few points and then connect them to form a smooth curve. Plotting these points and connecting them, we get a curve that decreases rapidly as x increases.
Now, to graph the reflection of f(x) about the line y = x, we need to swap the x and y values. The reflected function is given by g(x) = log0.5(5/x).
To find the x-intercept of the reflection, we set g(x) = 0 and solve for x:
log0.5(5/x) = 0
0.5^0 = 5/x
1 = 5/x
x = 5
So the x-intercept of the reflection is x = 5.
To prove that a^x = e^(x * ln(a)), we start with the definition of logarithms:
y = loga(b) if and only if a^y = b
Let’s set y = ln(a^x):
ln(a^x) = x * ln(a)
Now, let’s raise both sides to the power of e:
e^(ln(a^x)) = e^(x * ln(a))
Using the property that e^(ln(x)) = x, we have:
a^x = e^(x * ln(a))
Therefore, we have proved that a^x = e^(x * ln(a)).
3.How long will it take before twenty percent of our 1,000-gram sample of uranium-235 has decayed? [See Section 6.6 Example 13]. The decay equation is A(t)=A_0e^{Kt} , where t is the time for the decay, and K is the characteristic of the material. Suppose T is the time it takes for half of the unstable material in a sample of a radioactive substance to decay, called its half-life. Prove that K= \frac{ln0.5}{T} . What is K for the uranium-235? Show the steps of your reasoning. (T = 703,800,000 years)
To prove that K = ln(0.5)/T, we need to use the concept of half-life.
The half-life of a radioactive substance is the time it takes for half of the substance to decay. In other words, if we start with an initial amount A0, after one half-life, the amount remaining is A0/2.
Using the decay equation A(t) = A0e^(Kt), we can substitute t = T and A(t) = A0/2:
A0/2 = A0e^(KT)
Dividing both sides by A0:
1/2 = e^(KT)
Taking the natural logarithm of both sides:
ln(1/2) = ln(e^(KT))
Using the property ln(a^b) = b * ln(a):
ln(1/2) = KT * ln(e)
Since ln(e) = 1:
ln(1/2) = KT
Rearranging the equation to solve for K:
K = ln(1/2)/T
Simplifying ln(1/2):
K = ln(0.5)/T
Therefore, we have proved that K = ln(0.5)/T.
For uranium-235, given T = 703,800,000 years, we can substitute this value into the equation:
K = ln(0.5)/703,800,000
Calculating this value using a calculator or computer software, we find that K ≈ -10^9.
