1.What can be said about the domain of the function f ∘ g where f(y) = 4/(y-2) and g(x) = 5/(3x-1)? Express it in terms of a union of intervals of real numbers. Go to www.desmos.com/calculator and obtain the graph of f, g, and f ∘ g .
To determine the domain of the composite function f ∘ g, we need to consider the restrictions imposed by both functions f and g.
Let’s start with the function g(x) = 5/(3x – 1). The only restriction here is that the denominator (3x – 1) cannot be equal to zero, as division by zero is undefined. So, we solve the equation 3x – 1 = 0 to find the value that makes the denominator zero:
3x – 1 = 0
3x = 1
x = 1/3
Therefore, x cannot be equal to 1/3. We can express the domain of g as the set of all real numbers except x = 1/3.
Moving on to the function f(y) = 4/(y – 2), there is no restriction on the denominator (y – 2) since division by zero is not an issue in this case. So, the domain of f is the set of all real numbers.
Now, for the composite function f ∘ g, we need to consider the values of x that are in the domain of g and the resulting values of y that are in the domain of f.
Since the domain of g is all real numbers except x = 1/3, we substitute the expression for g(x) into f(y) and solve for y:
f(g(x)) = f(5/(3x – 1))
= 4/((5/(3x – 1)) – 2)
= 4/((5 – 2(3x – 1))/(3x – 1))
= 4/((5 – 6x + 2)/(3x – 1))
= 4/((7 – 6x)/(3x – 1))
= 4(3x – 1)/(7 – 6x)
To find the domain of f ∘ g, we need to consider any values of x that would make the expression undefined. In this case, we need to make sure that the denominator of f ∘ g is not zero:
7 – 6x ≠ 0
Solving for x:
7 – 6x ≠ 0
6x ≠ 7
x ≠ 7/6
Therefore, x cannot be equal to 7/6. We can express the domain of f ∘ g as the set of all real numbers except x = 1/3 and x = 7/6, which can be written as the union of intervals:
(-∞, 1/3) ∪ (1/3, 7/6) ∪ (7/6, +∞)
So, the domain of the function f ∘ g, expressed as a union of intervals of real numbers, is (-∞, 1/3) ∪ (1/3, 7/6) ∪ (7/6, +∞).
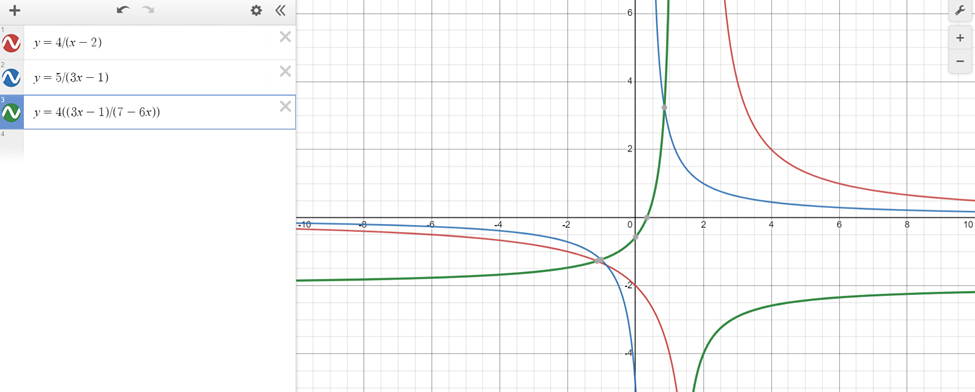
To obtain the graph of f, g, and f ∘ g in Desmos, I needed to follow these steps:
– To graph the function f(y) = 4/(y – 2), type “y = 4/(x – 2)” in the input bar.
– To graph the function g(x) = 5/(3x – 1), type “y = 5/(3x – 1)” in the input bar.
– To graph the composite function f ∘ g, type “y = 4((3x – 1)/(7 – 6x))” in the input bar.
The final graph looks as follows:
2. Find the inverse of the function f(x)=4+ √(x-2) . State the domains and ranges of both the function and the inverse function in terms of intervals of real numbers.
To find the inverse of a function, we need to switch the roles of x and y and solve for y. Let’s start by switching the variables:
x = 4 + √(y – 2)
Now, let’s solve for y:
x – 4 = √(y – 2)
Squaring both sides of the equation, we get:
(x – 4)2 = y – 2
Now, let’s isolate y:
y = (x – 4)2 + 2
So, the inverse of the function f(x) = 4 + √(x – 2) is:
f(-1)(x) = (x – 4)2 + 2
Now, let’s talk about the domains and ranges of both the function and its inverse.
For the function f(x) = 4 + √(x – 2), the domain is all real numbers greater than or equal to 2, since the square root requires a non-negative value inside. So, the domain is [2, ∞).
The range of the function f(x) is all real numbers greater than or equal to 4, since the square root will always produce a non-negative value. So, the range is [4, ∞).
For the inverse function f(-1)(x) = (x – 4)2 + 2, the domain is all real numbers, since there are no restrictions on the input.
The range of the inverse function f(-1)(x) is all real numbers greater than or equal to 2, since the square term (x – 4)2 will always be non-negative. So, the range is [2, ∞).
3. Go to www.desmos.com/calculator and obtain the graph of f , its inverse, and g(x)=x in the same system of axes. About what pair (a, a) are (11, 7) and (7, 11) reflected about?
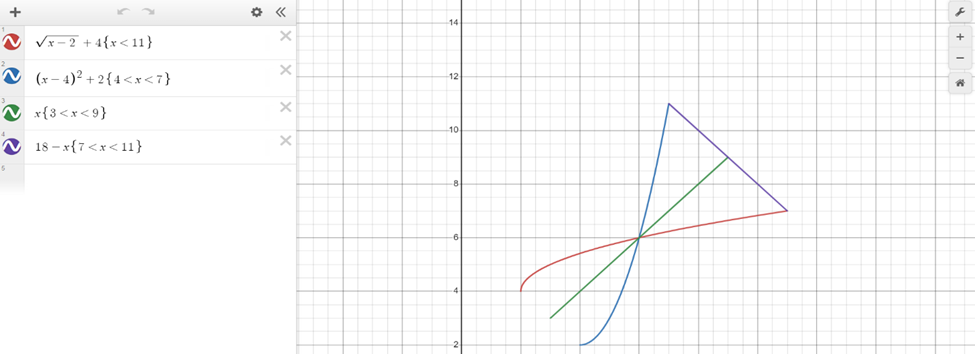
To obtain the graph of function f, its inverse f⁻¹, and the line g(x) = x in the same system of axes, we’ll first plot the points (11, 7) and (7, 11) and determine the line of reflection.
First, we need to plot the points (11, 7) and (7, 11) on the graph. Then, to find the line of reflection, we need to determine the midpoint between these two points. The midpoint is the average of the x-coordinates and the average of the y-coordinates.
The average of the x-coordinates is: (11 + 7) / 2 = 18 / 2 = 9
The average of the y-coordinates is: (7 + 11) / 2 = 18 / 2 = 9
So, the midpoint is (9, 9). This means that the points (11, 7) and (7, 11) are reflected about the line x = y, passing through the point (9, 9).
