1. Find the domain of the function using interval notation.
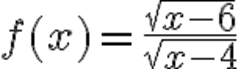
2. Sketch a graph of a piecewise function. Write the domain in interval notation.
3. The cost in dollars of making x items is given by the function C(x) = 10x + 500. a) The fixed cost is determined when zero items are produced. Find the fixed cost for this item. b) What is the cost of making 25 items? c) Suppose the maximum cost allowed is $1500. What are the domain and range of the cost function, C(x)?
1. Find the domain of the function using interval notation.
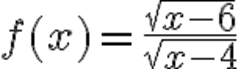
To find the domain of the function, we need to identify any values of x that would make the denominator equal to zero, since division by zero is undefined.
So, we set the denominator equal to zero and solve for x:
√(x-4) = 0
x-4 = 0 ; x = 4
Therefore, x cannot equal 4.
Next, we need to consider the square roots in the numerator and denominator. We know that the square root of a negative number is not a real number, so we need to ensure that the expression inside each square root is non-negative.
For the numerator:
x – 6 ≥ 0
x ≥ 6
For the denominator:
x – 4 ≥ 0
x ≥ 4
So, the domain of the function is all values of x greater than or equal to 6, except for x = 4:
Domain: [6, ∞) \ {4}
2. Sketch a graph of a piecewise function. Write the domain in interval notation.
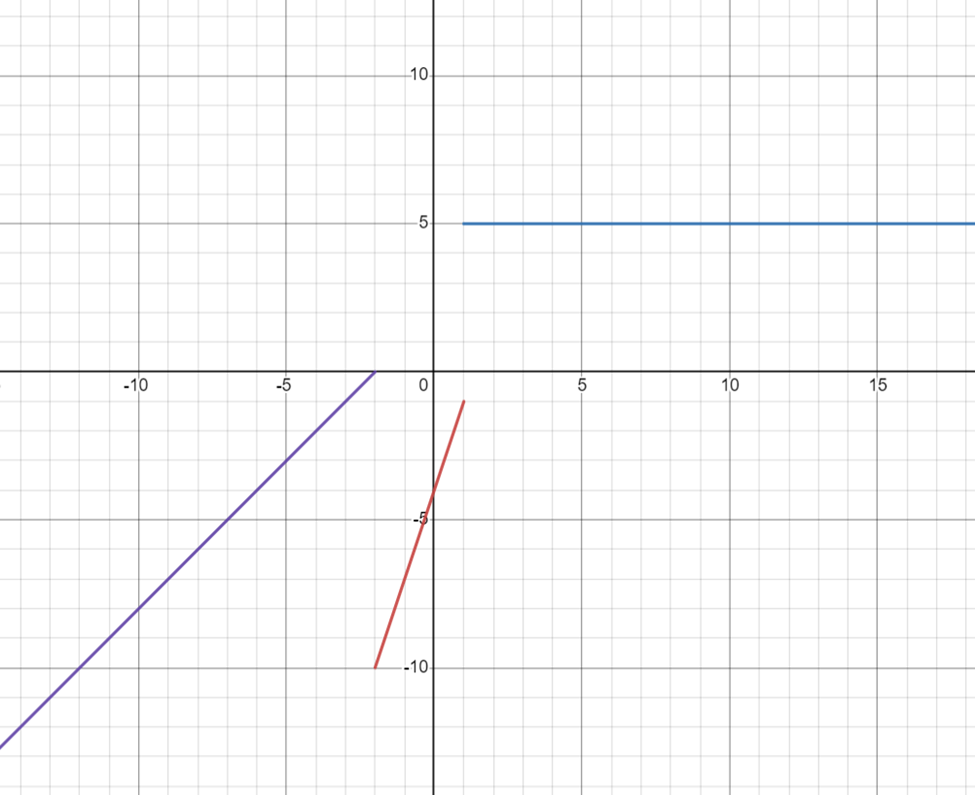
A piecewise function is a function that is defined by multiple sub-functions, where each sub-function is valid only on a certain interval or domain of the input values (MathIsFun, n.d.).
For this assignment, I chose the following piecewise function:
f(x) =
x + 2 if x < -2
3x – 4 if -2 <= x <= 1
5 if x > 1
This function is defined differently for different parts of its domain. When x is less than -2, f(x) is equal to x + 2. When x is between -2 and 1, f(x) is equal to 3x – 4. When x is greater than 1, f(x) is equal to 5.
The domain of this function is all real numbers, so we can represent it in interval notation as:
(-∞, -2) ∪ [-2, 1] ∪ (1, ∞)
This means that the function is defined for all real numbers except for -2 and 1, where there are gaps in the graph.
The graph will look as follows:
3. The cost in dollars of making x items is given by the function C(x) = 10x + 500.
a) The fixed cost is determined when zero items are produced. Find the fixed cost for this item.
The fixed cost is the cost that does not depend on the number of items produced (Hayes, 2023). In this case, the fixed cost is the constant term in the function C(x) when no items are produced, which is 500. Therefore, the fixed cost for this item is $500.
b) What is the cost of making 25 items?
To find the cost of making 25 items, we can use the function C(x) = 10x + 500 and substitute x = 25. So, C(25) = 10(25) + 500 = 750. Therefore, the cost of making 25 items is $750.
c) Suppose the maximum cost allowed is $1500. What are the domain and range of the cost function, C(x)?
The domain of the cost function C(x) is the set of all possible values of x, which represents the number of items produced. Since we cannot produce a negative number of items, the domain of C(x) is x ≥ 0.
The range of the cost function C(x) is the set of all possible values of C(x), which represents the cost of producing x items. Since the cost cannot be negative, the range of C(x) is C(x) ≥ 0.
Suppose the maximum cost allowed is $1500. We can set up an inequality to find the maximum number of items that can be produced within this cost limit:
10x + 500 ≤ 1500
Subtracting 500 from both sides, we get:
10x ≤ 1000
Dividing both sides by 10, we get:
x ≤ 100
Therefore, the domain of C(x) within the cost limit of $1500 is 0 ≤ x ≤ 100, and the corresponding range of C(x) is 500 ≤ C(x) ≤ 1500.
References
Hayes, A. (2023, April 21). Fixed Cost: What It Is and How It’s Used in Business. Retrieved from https://www.investopedia.com/terms/f/fixedcost.asp
MathIsFun. (n.d.). Piecewise Functions. Retrieved from https://www.mathsisfun.com/sets/functions-piecewise.html
