Consider the equation x^2+(y-2)^2=1 and the relation “(x, y) R (0, 2)”, where R is read as “has distance 1 of”. For example, “(0, 3) R (0, 2)”, that is, “(0, 3) has distance 1 of (0, 2)”. This relation can also be read as “the point (x, y) is on the circle of radius 1 with center (0, 2)”. In other words: “(x, y) satisfies this equation
x^2+(y-2)^2=1 , if and only if, (x, y) R (0, 2)”.
Does this equation determine a relation between x and y? Can the variable x can be seen as a function of y, like x=g(y)? Can the variable y be expressed as a function of x, like y= h(x)? If these are possible, then what will be the domains for these two functions? What are the graphs of these two functions? Are there points of the coordinate axes that relate to (0, 2) by means of R?
The equation x^2 + (y-2)^2 = 1 represents a circle centered at (0,2) with a radius of 1. The relation R between two points (x, y) and (0, 2) is defined as having a distance of 1 between them, which means that the two points lie on the circle.
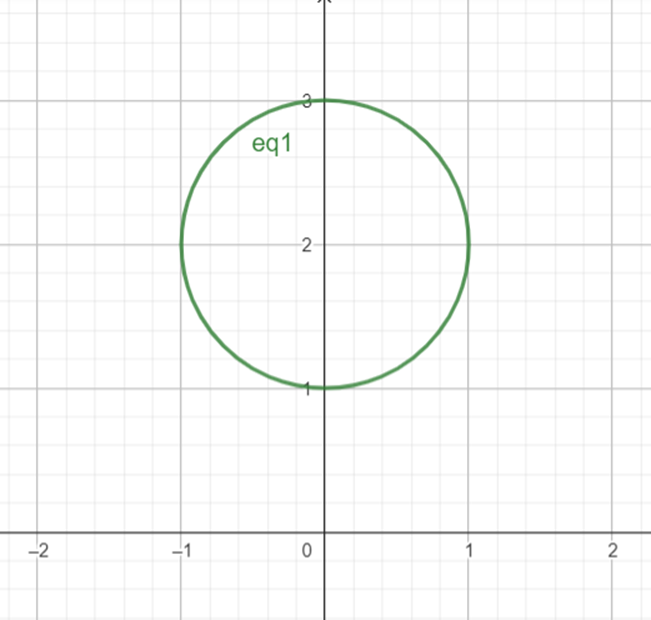
x^2 + (y-2)^2 = 1
Each potential input value in a function corresponds to only one output value (Abramson, 2017). Therefore, our equation does not determine a relation between x and y in the form of a function. This is because for each value of y, there are two possible values of x that satisfy the equation. For example, if y = 3, then x can be either -√(2) or √(2). Therefore, x cannot be seen as a function of y, and y cannot be expressed as a function of x.
However, we can express x in terms of y or vice versa by using the equation of the circle. Solving for x, we get x = ± √(1 – (y-2)^2). Similarly, solving for y, we get y = 2 ± √(1 – x^2).
The domain of x as a function of y is [-1, 1], since the value inside the square root cannot be negative. The domain of y as a function of x is [-√(2), √(2)], since the value inside the square root cannot be greater than 1.
The graph of x as a function of y would be two half-circles, one in the first quadrant and the other in the second quadrant, with a radius of √(1 – (y-2)^2) and centered at (0,2). The graph of y as a function of x would be two half-circles, one in the first quadrant and the other in the fourth quadrant, with a radius of √(1 – x^2) and centered at (0,2).
There are no points on the x-axis that are related to (0,2) by means of R, since the only points on the circle with a y-coordinate of 0 are (±1, 0), which are not related to (0,2) by R. However, there is one point on the y-axis that is related to (0,2) by means of R, which is (0,1). This point lies on the circle and has a distance of 1 from (0,2).
References
Abramson, J. (2017). Algebra and trigonometry. OpenStax, TX: Rice University. Retrieved from https://openstax.org/details/books/algebra-and-trigonometry
